Using the TI-89 to solve set of equations is very easy and can be performed using the simult() function. This function can be found by pressing catalog, then s ,and then scrolling down until you can find that exact function.
When using the simult() function, it is very helpful to have the rough matrix form in front of you, especially when you are first learning how to solve these problems using nodal analysis or mesh analysis.
Example: Using
nodal analysis
Perform the nodal analysis to derive a set of equations like:
Node Va: 4Va - Vb = 60
Node Vb: -Va
+ 4Vb = 60
Those will translate to the following matrix form:
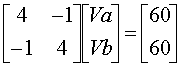
Using the TI-89, enter the following:
·
Simult(
[3,-1;-1,4],[60;60])
- Then press Enter
Notice that to separate the individual coefficients we use a comma. To indicate to the calculator that there is a break in the level of the matrix we use a semi-colon.
The answer should appear as:
![]() which means:
which means: ![]()
Example 2. Mesh analysis
Similarly, Mesh analysis problems can be solved in the same way as nodal.
From Example 4.7 page
80
Mesh 1: 3i1 i2 -2i3 = 1
Mesh 2: -i1 + 6i2 3i3 = 0
Mesh 3: -2i1 3i2 + 6i3 = 6
Which translates into this matrix:
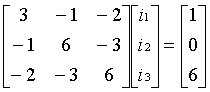
Using the TI-89, enter the following:
·
simult([3,-1,-2 ;
-1,6,-3 ; -2,-3,6],[ 1; 0 ; 6])
- Then press Enter
The answer will appear as:
![]() which translates to i1 = 3, i2
= 2, i3= 3
which translates to i1 = 3, i2
= 2, i3= 3
For further reference on this or any other functions in your TI-89, check out the online guide at:
http://education.ti.com/us/product/tech/89/guide/89guideus.html